Galois connections

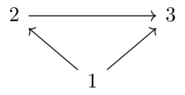
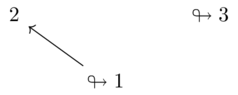
Definition and examples(5)
Exercise 1-101(2)

Does \(\mathbb{R}\xrightarrow{\lceil x/3 \rceil}\mathbb{Z}\) have a left adjoint \(\mathbb{Z} \xrightarrow{L} \mathbb{R}\)? If not, why? If so, does its left adjoint have a left adjoint?

Solution(1)

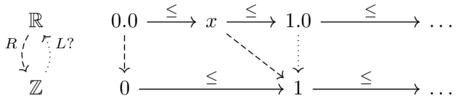
  • Assume we have an arbitrary left adjoint, \(L\).

  • For \(x\) as it approaches \(0.0 \in \mathbb{R}\) from the right, we have \(R(x) \leq 1\), therefore \(L(1) \leq x\) because \(L\) is left adjoint.

  • Therefore \(L(1)\leq 0.0\), yet this implies \(R(0.0) \leq 1\).

  • This contradicts \(R(0.0)=0\), therefore no left adjoint exists.

Floor and ceil(1)

  • Consider the map \(\mathbb{Z} \xrightarrow{3z} \mathbb{R}\) which sends an integer to \(3z\) in the reals.

  • To find a left adjoint for this map, we write \(\lceil r \rceil\) for the smallest natural above \(r \in \mathbb{R}\) and \(\lfloor r \rfloor\) for the largest integer below \(r \in \mathbb{R}\)

  • The left adjoint is \(\lceil r/3 \rceil\)

  • Check: \(\lceil x/3 \rceil \leq y\) \(\iff x \leq 3y\)

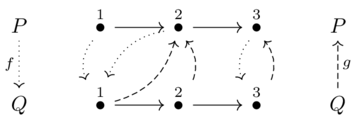
Galois connection(1)
Total order galois connections(1)

  • Consider the total orders \(P = Q = \underline{3}\) with the following monotone maps:

  • These maps do not form a Galois connection:

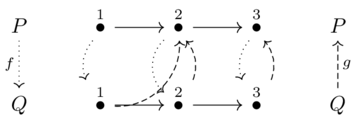
    • These do not because of \(p=2, q = 1\)

    • \(f(p)=2 \not \leq q=1\) which is not the same as \(p = 1 \leq g(q)=2\)

  • In some sense that can be formalized, for total orders the notion of Galois connection corresponds to the maps not ‘crossing over’.

Back to partitions(3)
Exercise 1-106(2)

Given a function \(\{1 \mapsto 12, 2 \mapsto 12, 3 \mapsto 3, 4 \mapsto 4\}\) from the four element set \(S\) to the three element set \(T\)

  1. Choose a nontrivial partition \(c \in Prt(S)\) and compute \(g_!(c) \in Prt(T)\)

  2. Choose any coarser partition \(g_!(c)\leq d \in Prt(T)\)

  3. Choose any non-coarser partition \(g_!(c) > e \in Prt(T)\)

  4. Find \(g^*(d)\) and \(g^*(e)\)

  5. Show that the adjunction formula is true, i.e. that \(c \leq g^*(d)\) (because \(g_!(c) \leq d\)) and \(g^*(e) > c\) (because \(e > g_!(c)\))

Solution(1)

  1. \(c = \{(1, 3),(2,), (4,)\}\), \(g_!(c)\) is then \(\{(12,3),(4,)\}\)

  2. \(d = \{(12,),(3,),(4,)\}\)

  3. \(e = \{(12,3,4)\}\)

  4. \(g^*(d)=\{(1,2),(3,),(4,)\}, g^*(e)=\{(1,2,3,4)\}\)

  5. \(c \leq g^*(d)\) and \(g^*(e) > c\)

Basic theory of Galois connections(12)
Galois connection alternate form(2)

Suppose \(P \overset{g}{\underset{f}{\leftrightarrows}} Q\) are monotone maps. The following are equivalent:

Proof(1)

  • Forward direction

    • Take any \(p \in P\) and let \(q = f(p) \in Q\)

      • By reflexivity, we have in \(Q\) that \(f(p) \leq q\)

      • By definition of Galois connection, we then have \(p \leq g(q)\), so (1) holds.

    • Take any \(q \in Q\) and let \(p = g(q) \in P\)

      • By reflexivity, we have in \(P\) that \(p \leq g(q)\)

      • By definition of Galois connection, we then have \(f(p) \leq q\), so (2) holds.

  • Reverse direction

    • Want to show \(f(p)\leq q \iff p \leq g(q)\)

    • Suppose \(f(p) \leq q\)

      • Since g is monotonic, \(g(f(p)) \leq g(q)\)

      • but, because (1), \(p \leq g(f(p))\), therefore \(p \leq g(q)\)

    • Suppose \(p \leq g(q)\)

      • Since f is monotonic, \(f(p) \leq f(g(q))\)

      • but, because (2), \(f(g(q)) \leq q\), therefore \(f(p) \leq q\)

Linked by

Adjoints preserving meets and joins(2)

  • Let \(P \overset{f}{\underset{g}{\rightleftarrows}} Q\) be monotone maps with \(f \dashv g\).

  • Right adjoints preserve meets

    • Suppose \(A \subseteq Q\) is any subset and \(g(A)\) is its image.

    • Then, if \(A\) has a meet \(\wedge A \in Q\), then \(g(A)\) has a meet \(\wedge g(A) \in P\)

    • And \(g(\wedge A) \cong \wedge g(A)\)

  • Left adjoints preserve joins

    • Given \(A \subseteq P\) and its image \(f(A) \subseteq Q\)

    • Then, if \(A\) has a join \(\vee A \in P\), then \(\vee f(a) \in Q\) exists

    • And \(f(\vee A) \cong \vee f(A)\)

Proof(1)

  • Left adjoints preserve joins

    • let \(j = \vee A \subseteq P\)

    • Given f is monotone, \(\forall a \in A: f(a) \leq f(j)\), i.e. we have \(f(a)\) as an upper bound for \(f(A)\)

    • To show it is a least upper bound, take some arbitrary other upper bound b for \(f(A)\) and show that \(f(j) \leq b\)

      • Because \(j\) is the least upper bound of \(A\), we have \(j \leq g(b)\)

      • Using the Galois connection, we have \(f(j) \leq b\) showing that \(f(j)\) is the least upper bound of \(f(A) \subseteq Q\).

  • Right adjoints preserving meets is dual to this.

Linked by

Adjoint functor theorem for preorders(2)
Proof(1)

  • Given a right adjoint, construct the left adjoint by:

    • \(f(p) := \bigwedge\{q \in Q\ |\ p \leq g(q)\}\)

    • First need to show this is monotone:

      • If \(p \leq p'\), the relationship between the joined sets of \(f(p)\) and \(f(p')\) is that the latter is a subset of the former.

      • By Proposition 1.91 we infer that \(f(p) \leq f(p')\).

    • Then need to show that it is satisfies the left adjoint property:

      • Show that \(p_0 \leq g(f(p_0))\)

        • \(p_0 \leq \bigwedge \{g(q)\ |\ p_0 \leq g(q)\} \cong g(\bigwedge\{q\ |\ p_0 \leq g(q)\}) = g(f(p_0))\)

        • The first inequality comes from the fact that the meet of the set (of which \(p_0\) is a lower bound) is a greatest lower bound.

        • The congruence comes from the fact that right adjoints preserve meets.

      • Show that \(f(g(q_0)) \leq q_0\)

        • \(f(g(q_0)) = \bigwedge\{q\ |\ g(q_0) \leq g(q)\} \leq \bigwedge \{q_0\} = q_0\)

        • The first inequality comes from Proposition 1.91 since \(\{q_0\}\) is a subset of the first set.

        • The second equality is a property of the meet of single element sets.

  • Proof of a left adjoint construction (assuming it preserves joins) is dual.

Linked by

Adjoints in Set(1)

  • Let \(A \xrightarrow{f} B\) be a set function, say between apples and buckets into which we put each apple.

  • The ‘pullback along f’ \(\mathbb{P}(B) \xrightarrow{f^*} \mathbb{P}(A)\) maps each subset \(B' \subseteq B\) to its preimage \(f^{-1}(B') \subseteq A\)

    • It tells you for a set of buckets all the apples contained in total.

    • It is a monotonic map which has a left and right adjoint: \(f_! \dashv f^* \dashv f_*\)

  • The left adjoint \(\mathbb{P}(A)\xrightarrow{f_!}\mathbb{P}(B)\) is given by the direct image

    • \(f_!(A') := \{b \in B\ |\ \exists a \in A': f(a)=b\}\)

    • Tells you for a set of apples all the buckets that contain at least one of those apples.

  • The right adjoint \(\mathbb{P}(A) \xrightarrow{f_*} \mathbb{P}(B)\) is defined as follows:

    • \(f_*(A') := \{b \in B\ |\ \forall a: f(a)=b \implies a \in A'\}\)

    • Tells you all the buckets which are all-\(A\prime\) (note that empty buckets vacuously satisfy this condition).

  • Adjoints often turn out to have interesting semantic interpretations.

Exercise 1-110(2)

Show that if \(P \xrightarrow{f}Q\) has a right adjoint g, then it is unique up to isomorphism. Is the same true for left adjoints?

Solution(1)

  • Suppose \(h\) is also right adjoint to \(f\).

  • What it means for \(h \cong g\):

    • \(\forall q \in Q: h(q) \cong g(q)\)

  • \(g(q) \leq h(q)\)

    • Substitute \(g(q)\) for \(p\) in \(p \leq h(f(p))\) (from \(h\)’s adjointness) to get \(g(q) \leq h(f(g(q)))\)

    • Also apply \(h\) to both sides of \(f(g(q)) \leq q\) (from \(g\)’s adjointness) to get \(h(f(g(q)))\leq h(q)\)

    • The result follows from transitivity.

  • By symmetry (nothing was specified about \(h\) or \(g\)) the proof of \(h(q)\leq g(q)\) is the same.

  • Same reasoning for left adjoints.

Exercise 1-118(2)

Choose sets \(X,Y\) with between two and four elements each, and choose a function \(X \xrightarrow{f} Y\) NOCARD

  1. Choose two different subsets \(B_1, B_2 \subseteq Y\) and find \(f^*(B_1)\) and \(f^*(B_2)\)

  2. Choose two different subsets \(A_1, A_2 \subseteq X\) and find \(f_!(A_1)\) and \(f_!(A_2)\)

  3. With the same \(A_1, A_2\) find \(f_*(A_1)\) and \(f_*(A_2)\)

Solution(1)

\(\bar 3 \xrightarrow{f} \bar 4\) with \(\{1 \mapsto 2, 2 \mapsto 2, 3\mapsto 4\}\),\(A_1 = \{1,2\}, A_2=\{2,3\}, B_1=\{1\}, B_2=\{1,4\}\)

  1. \(f^*(B_1)=\varnothing, f^*(B_2)=\{4\}\)

  2. \(f_!(A_1)=\{2\},f_!(A_2)=\{2,4\}\)

  3. \(f_*(A_1)=\{1,2,3\},f_*(A_2)=\{1,3,4\}\)

Closure operators(7)

Given a Galois connection we can compose the left and right maps to get a closure operator

Closure operator(1)

A closure operator \(P \xrightarrow{j} P\) on a preorder \(P\)

A monotone map such that for all \(p \in P\) we have:

  1. \(p \leq j(p)\)

  2. \(j(j(p)) \cong j(p)\)

Linked by

Eval as closure(1)

  • Example of a closure operator

  • Think of the preorder of arithmatic expressions such as \(12, 4+2+4, 9*(2+3)\), where the \(\leq\) operators denotes whether an expression can be simplified to another.

  • A computer program \(j\) that evaluates expressions is a monotonic function on the preorder to itself (if you can reduce x to y, then \(j(x)\) should be able to be rewritten as \(j(y)\).

  • The requirements of closure operator say that \(j\) should be a simplification, and that trying to reduce an expression which has already been reduced will do nothing further.

Adjunctions from closures(1)

  • Just as adjunctions give rise to closure operators, from every closure operator we may construct an adjunction.

  • Let \(P \xrightarrow{j} P\) be a closure operator.

  • Get a new preorder by looking at a subset of \(P\) fixed by \(j\).

    • \(fix_j\) defined as \(\{p \in P\ |\ j(p)\cong p\}\)

  • Define a left adjoint \(P \xrightarrow{j} fix_j\) and right adjoint \(fix_j \xhookrightarrow{g} P\) as simply the inclusion function.

  • To see that \(j \dashv g\), we need to verify \(j(p) \leq q \iff p \leq q\)

    • Show \(\rightarrow\):

      • Because \(j\) is a closure operator, \(p \leq j(p)\)

      • \(j(p) \leq q\) implies \(p \leq q\) by transivity.

    • Show \(\leftarrow\):

      • By monotonicity of \(j\) we have \(p \leq q\) implying \(j(p) \leq j(q)\)

      • \(q\) is a fix point, so the RHS is congruent to \(q\), giving \(j(p) \leq q\).

Closures in logic(1)

  • Examples of closure operators from logic.

  • Take set of all propositions as a preorder, where \(p \leq q\) iff \(p\) implies \(q\).

  • Some modal operators are closure operators

  • E.g. \(j(p)\) means “Assuming Bob is in Chicago, p”

    • \(p \implies j(p)\) (the logic is monotonic, adding assumptions does not make something true into something false.

    • \(j(j(p)) = j(p)\) (the assumption is idempotent)

Exercise 1-119(2)

Given \(f \dashv g\), prove that the composition of left and right adjoint monotone maps is a closure operator

  1. Show \(p \leq (f;g)(p)\)

  2. Show \((f;g;f;g)(p) \cong (f;g)(p)\)

Solution(1)

  1. This is one of the conditions of adjoint functors: \(p \leq g(f(p))\)

    • The \(\leq\) direction is an extension of the above: \(p \leq g(f(p)) \leq g(f(g(f(p))))\)

    • Galois property: \(q \geq f(g(q))\), substitute \(f(p)\) for \(q\) to get \(f(p) \geq f(g(f(p)))\).

    • Because \(g\) is a monotone map, we can apply it to both sides to get \(g(f(p)) \geq g(f(g(f(p))))\)

Level shifting(3)
Preorder of relations(1)

  • ‘Level shifting’

  • Given any set \(S\), there is a set \(\mathbf{Rel}(S)\) of binary relations on \(S\) (i.e. \(\mathbb{P}(S \times S)\))

  • This power set can be given a preorder structure using the subset relation.

  • A subset of possible relations satisfy the axioms of preorder relations. \(\mathbf{Pos}(S) \subseteq \mathbb{P}(S \times S)\) which again inherits a preorder structure from the subset relation

    • A preorder on the possible preorder structures of \(S\), that’s a level shift.

  • The inclusion map \(\mathbf{Pos}(S) \hookrightarrow \mathbf{Rel}(S)\) is a right adjoint to a Galois connection, while its left adjoint is \(\mathbf{Rel}(S)\overset{Cl}{\twoheadrightarrow} \mathbf{Pos}(S)\) which takes the reflexive and transitive closure of an arbitrary relation.

Exercise 1-125(2)

Let \(S=\{1,2,3\}\)

  1. Come up with any preorder relation on \(S\), and define \(U(\leq):=\{(s_1,s_2)\ |\ s_1 \leq s_2\}\) (the relation ‘underlying’ the preorder. Note \(\mathbf{Pos}(S) \xhookrightarrow{U} \mathbf{Rel}(S)\))

  2. Pick binary relations such that \(Q \subseteq U(\leq)\) and \(Q' \not \subseteq U(\leq)\)

We want to check that the reflexive/transitive closure operation \(Cl\) is really left adjoint to the underlying relation \(U\).

  • The meaning of \(Cl \dashv U\) is \(Cl(R) \sqsubset \leq \iff R \sqsubset U(\leq)\), where \(\sqsubset\) is the order relation on \(\mathbf{Pos}(S)\)

  1. Concretely show that \(Cl(Q) \sqsubset \leq\)

  2. Concretely show that \(Cl(Q') \not \sqsubset \leq\)

Solution(1)

  1. Let the preorder be given by this diagram (with implicit reflexive arrows):

  2. Let \(Q\) be given by the following diagram

    • and let \(Q'=S\times S\)

  3. \(Cl(Q) = \{11,12,22,33\}\) \(\sqsubset\) \(\leq = \{11,22,33,12,23,13\}\)

  4. \(Cl(Q') = Q' = S \times S\) \(\not \sqsubset\) \(\leq\) (reason: \((3,1) \in S \times S\) but \((3,1) \not \in \leq\))